The article below suggests you about the determinant calculators and its use. Also, a detailed description of how to solve the linear and vector equations will get mentioned in the article. The 2x2, 3x3, and 4x4 matrix det(A) solutions are also present in the content.

The calculator and its use have got mentioned if you find it difficult to solve them by hand. Also, the article tells you about how to proceed with the det(A) finder. It’s a course material that was prepared for the twelfth standard students and even for higher studies. Read the article more to know more about the equations and the solutions.

The determinant calculator

So, today we’ll be discussing the matrix, determinant calculator (calc). The concept of determinants and the matrices has excelled in every field of science. It helps in solving not just linear equations but vector and scalar products too. We are all aware of the linear equations and they might have a single or infinite set of solutions. Now, what are determinants? What is a matrix of a determinant? Answers to these questions would come up next in the article.

The determinants are equivalent to the squared matrix with real elements. It gets denoted by det (A), |A|, and det A. They are used to solve the linear equations and hence find the uncertain variables. Likewise, a det(A) of a 2x2 of matrix A will be: , which is deserved as

Now, the matrices got denoted by square brackets, but the determinant stands for vertical bars. The det(A) will be a single number to the array of matrices’ digits. Also, this calculator got designed to find det(A) for the matrix values like 2x2, 3x3, and 4x4.

How to find the determinant of a matrix calculator?

As we now know what is a det(A) and now we will learn how to find matrix determinant. The following steps will tell you how to incorporate the values and find the solutions. They are: · Firstly, let us take an example for the 2x2 matrix for det A. Now, if
Then the result will be:

• So, as you see the above example, you could notice what one has done.
• Rule no.1: You must use multiple the values in the first row and first column to the element in the second row and second column.
• Rule no.2: Then, it would help if you multiplied the value in the second row and second column to the first row and first column.
• The above points can be simple, defined as the difference between the first and the second product. Also, this was the example of 2x2 matrix values.
• Now, next up is coming for the det(A) of the 3x3 and 4x4 matrix.

Know the minors

How to know the minors? Minors got defined for an nxn matrix det(A) as (n-1)x(n-1). For a better understanding, let’s assume, we have a 3x3 matrix det(A). Now, we temporarily remove the third column and row, then the rest of the elements would get considered as minors.

Now, in order to evaluate the nxn matrix then, one must expand the det(A) by the minors. Firstly, what we do is that we select a row and then start the multiplication. Secondly, we multiply the position sign, minors, and the elements of the row we decided. You’ll see in the examples below about how to increase and evaluate the solution. What you do need to remember is that you must remember the sign conventions, which is also mentioned later in the article.

As already mentioned that for a 4x4 det(A), the 3x3 det(A) is the minors. After you choose the row or a column, each element of it must get multiplied by -1 or +1. They are depending upon whether the summation of the row and the column elements is even or odd. Hence, the product of a minor component and a number, +1 or -1 is known as Cofactors.

The determinant calculator 3x3

The 3x3 determinant calculators of a matrix got defined as
, which is derived as

As you see the derivation let us now look at the example, which lies below: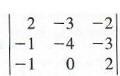
Far, after this, extend the second column. Also, remember you must get the minor elements, 2x2, into the second column like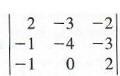
Now, start to cofactor these results like

The determinant calculator 4x4

We have seen derivations above with examples, of course. But now we will see the case of a determinant solver for 4x4.

First of all, let us look at the example what we need to evaluate:
,where you expand the fourth row with the minors like

• Now, each of the determinants in the above example has to get expanded with the three minors.
• Also, make sure to solve the det(A) with more zeroes first as it might make the equation simpler to solve.
• Although it is easy to settle with the determinant calculator.
• The determinant finder can also deal with the real world problematic equations in all fields of science. As it might solve the vector and the scalar equations too.

How to use the matrix determinant calculator?

The following steps would suggest to you how to use the matrix determinant calculator, and they are as follows:

• As mentioned above, the matrices contain real numbers and so put the values in the calc.
• After placing all the matrix values in the box, push the “Generate Work” button, so it starts solving.
• The result will also be a real number that will provide you with a lot of information about the equation.