Trapezoidal Rule Calculator
Overview of Trapezoidal Rule Calculator:
A simple calculator made for students, mathematicians, teachers and researchers. This Trapezoidal Rule calculator takes the function as input and gives the solution. The Trapezoidal Rule Calculator is all-in-one calculator it not only calculates area but also the error.
What is Trapezoidal Rule?:
Before integration, mathematicians used to wonder how to calculate the area under the parabola. A parabola is a curve on a plane. Since it is easy to calculate the area of a rectangle, mathematicians would divide the curve into different rectangular segments. But soon they realised that it was not a proper way to do it. There is some area which is not considered or should not be considered. As you can see from the below graph, when drawing a rectangle, the top corners are either outside or inside. Hence they could not calculate more accurately.

By drawing trapezoid instead of rectangle, we can get more accurate result. The Trapezoidal Rule is based on Newton-Cotes Formula which is as follows:
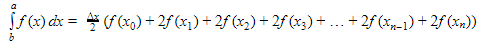
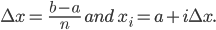

The results can be improved by partitioning the integration interval and using the trapezoidal rule to all subintervals and summing up the results.
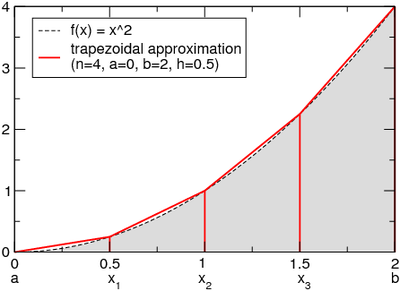
Example of How-to Use The Trapezoidal Rule Calculator:
Consider the function
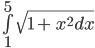
calculate the area under the curve for n=8. Enter the function and limits on the calculator and below is what happens in the background. Solution: Given that n=8 we have

Hence we will be plotting intervals are 0.5 gaps. Now we will calculate area for each trapezoid, i.e, for x0, x1 ,x2, x3, x4, x5, x6, x7. x0=1.
 =
=
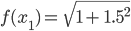 =
=
 =
=
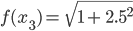 =
=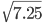
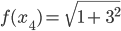 =
=
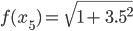 =
=
 =
=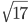
 =
=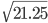
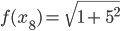 =
=
Now Applying the Trapezoid Rule formula:
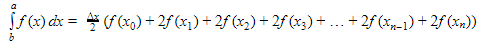

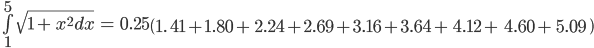

Alternative methods to Trapezoidal Rule:
There are many other methods alternative to Trapezoidal Rule and
share the common family of numeral integrals. The Simpson’s Rule
is another effective method and has faster convergence than the
former for continuously differentiable functions, though not in
all cases.
Trapezoidal is nearly accurate when used on
periodic functions which are integrated over periodic intervals.
For non-periodic functions, like the Gaussian quadrature and
Clenshaw-Curtis quadrate with an unequally spaced point are more
accurate.