Simpson's Rule Calculator- Mathauditor

Simpson's rule Calculator

Simpson’s rule is a technique to calculate the approximation of definite curve and is used to find area beneath or above the parabola. We have formulas to find the area of a shape, a polygon (having more than 2 sides). But in order to find the area beneath the curve, we use Simpson’s Rule. The Simpson’s rule formula states that the curve will be divided into n equal vertical parts. Then each part is taken and its area is calculated.
We divide the area into n equal segments of width Δx. The approximate area is given by the following.

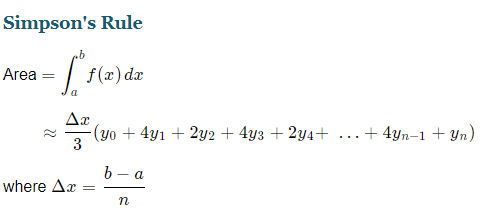
and n is even.
Which this can be further simplified to Simpson’s 1/3 Rule:

The Simpson’s Rule is a credit to Thomas Simpson (1710-1761), a mathematician, but Johannes Kepler used such similar formula over 100 years prior to him. Hence this method is sometimes known as by Kepler’s Rule.
There is a variation in Simpson’s rule, which is based on cubic interpolation rather than a quadratic interpolation. The Simpson’s 3/8 Rule is as follows:

Where epsilon ԑ, is some number between a and b. This method is as twice accurate as the standard method. Although it uses one more function value.

How do we calculate Simpson’s Rule?

We are given a curve whose area we need to find. A function is given, with values of a and b. The n is the number of segments to be created for Simpson’s Rule calculation. Then we perform the following steps:
Step 1: We divided it into n equal parts. Point to remember, it must be even for Simpson’s Rule. More the segments, the accuracy of the result increases.

Step 2: we construct a parabola which nearly matches the curve in each of the segments. This will give you the idea of the parabola whose area you are about to calculate.
Step 3: Take two segments starting from left, we take two endpoints and a middle point.

Step 4: Apply Simpson’s rule formula and calculate the area of the curve. But since the area is an approximate value, we will also need to calculate the error.

Example for How-to Use Simpson’s Rule Calculator:

Approximate

using Simpson's Rule with n=4; Enter this Function in our calculator and below is what happens in the background.

First we calculate value of Δx

Δx=

Further, we will calculate the value of

we will start with

in the function and then incremented by the value of Δx by 0.25 till x tends to 3.

	y0  = f(a)
		= f(2)=
		= 0.333333…

	y1=fa+Δx 

	



	y2=f(a+2Δx ) 
	

	y3=f(a+3Δx ) 
	

	y4=f(b)

Now since we have all the values we will calculate the area of the curve.
Applying Simpson’s Rule:
Area =

Hence the area beneath the curve is 0.2876.
This is how we calculate using Simpson’s Rule Calculator. The answer of the above function if calculated with Trapezoidal Rule the value is: 0.287682 so our Simpson’s Rule has an error of approximate 0.00036%.
Our Simpson’s Rule Calculator not only calculates the area beneath the curve but also calculates the Error.

Simpson Rule Calculator